双曲线是高中数学中的重要概念之一,它有着广泛的应用背景,例如物体运动、电磁场分布等。掌握双曲线公式不仅对于理解数学知识体系有着重要意义,更为今后的学习和工作提供了坚实的基础。本文将全面高中数学双曲线公式,帮助读者深入理解和应用。

一、直角坐标系下的双曲线公式
这一部分将介绍直角坐标系下常见的双曲线公式,包括椭圆、双曲线、抛物线等,并详细讲解它们的定义、性质和图像特点。
二、焦点与准线的关系
焦点与准线是双曲线中的两个重要概念,它们的位置与双曲线的形状密切相关。本部分将介绍焦点与准线的定义和计算方法,并通过实例演示它们之间的关系。
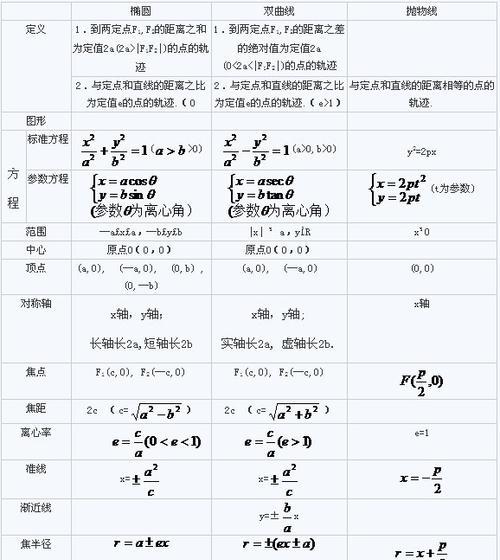
三、双曲线的标准方程
双曲线的标准方程是双曲线公式的一种重要形式,它可以简洁地描述双曲线的性质和特点。本部分将详细介绍双曲线的标准方程的推导和应用。
四、双曲线的参数方程
双曲线的参数方程是另一种常见的表达方式,它以参数形式给出了双曲线上的点的坐标。这一部分将讲解双曲线的参数方程的推导和使用方法,并通过实例展示其应用场景。
五、双曲线的离心率与焦距
离心率与焦距是衡量双曲线形状和位置的两个重要指标。本部分将介绍离心率和焦距的定义、计算方法以及它们与双曲线图像之间的关系。

六、双曲线的渐近线
双曲线的渐近线是与双曲线图像有着密切联系的一条直线,它具有一些特殊的性质。这一部分将详细介绍渐近线的定义、判定方法和图像特点,并解答读者常见的疑问。
七、双曲线的对称轴
对称轴是双曲线的一个重要几何元素,它具有对称性,并且对于双曲线的图像有着重要的影响。本部分将讲解对称轴的定义、计算方法以及与双曲线图像之间的关系。
八、双曲线的中心和顶点
双曲线的中心和顶点是双曲线图像中的两个重要点,它们的位置与双曲线的形状密切相关。这一部分将详细介绍中心和顶点的定义、计算方法以及它们与双曲线图像之间的关系。
九、双曲线的参数方程推导
本部分将介绍双曲线参数方程的推导过程,帮助读者深入理解参数方程的含义和作用,并通过实例演示参数方程在解决实际问题中的应用。
十、双曲线与圆锥曲线
双曲线与圆锥曲线是数学中常见的两类曲线,它们有着一些共同特点和不同之处。本部分将比较双曲线与圆锥曲线的性质和公式,并通过实例解释它们的联系和区别。
十一、高中数学中的双曲线应用
双曲线在高中数学中的应用非常广泛,例如解析几何、物理等领域都能看到双曲线的身影。本部分将介绍双曲线在高中数学中的常见应用,并通过实例讲解其具体应用方法。
十二、双曲线公式的简化与推广
双曲线公式的简化和推广是进一步研究双曲线的基础,也是掌握双曲线公式的关键。本部分将讲解如何通过简化和推广双曲线公式来深入理解和应用双曲线。
十三、常见双曲线公式
通过前面的内容,本部分将常见的双曲线公式,以便读者能够快速查阅和应用。
十四、双曲线公式的证明
本部分将简要介绍双曲线公式的证明过程,帮助读者理解双曲线公式的起源和原理,并提供相关的参考文献供读者进一步研究。
十五、结语:掌握双曲线公式,驾驭数学世界
通过本文的学习,相信读者已经对高中数学中的双曲线公式有了更深入的理解。双曲线作为数学中的重要概念之一,不仅在学术研究中有着广泛应用,也与现实生活密切相关。掌握双曲线公式,将帮助我们更好地理解和应用数学知识,提升数学思维能力,驾驭数学世界。
标签: 双曲线公式

